407. Trapping Rain Water II

Hard

Description

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

Example 1:

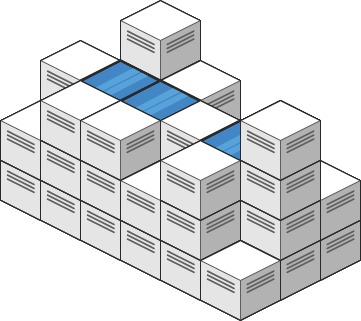
Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

Solutions

Approach: BFS + Priority Queue (Min Heap)

Time complexity: \(O(mn \log mn)\)

Space complexity: \(O(mn)\)

Way 1:

Algorithmic Way

The problem requires finding the volume of water that can be trapped given a 2D elevation map.

We use a min-heap \(\textit{pq}\) to always process the lowest boundary first, which allows us to determine how much water can be trapped above it.

We initialize the heap \(\textit{pq}\) with all boundary cells and mark them as visited in set \(\textit{vis}\). Then, we process each cell by popping from the heap, checking its neighbors, and calculating trapped water if applicable. The neighbors are pushed into the heap if they haven't been visited yet, and we update the maximum height seen so far to calculate water trapping correctly.

The time complexity is \(O(mn \log mn)\), where \(n\) is the number of rows and \(m\) is the number of columns in the heightMap array. Each cell is pushed and popped from the heap once, and heap operations take \(O(\log mn)\) time.

The space complexity is \(O(mn)\), for storing the visited \(\textit{vis}\) set and the priority queue \(\textit{pq}\), which can grow up to the size of all the cells in the grid.

Python

class Solution:
    def trapRainWater(self, heightMap: List[List[int]]) -> int:
        if not heightMap or not heightMap[0]:
            return 0
        m, n = len(heightMap), len(heightMap[0])
        pq = []     #min heap
        vis = set()
        # Push all the boundary cells into the heap(aka priority queue)
        for i in range(m):
            heappush(pq, (heightMap[i][0], i, 0))
            heappush(pq, (heightMap[i][n-1], i, n-1))
            vis.add((i, 0))
            vis.add((i, n-1))

        for j in range(n):
            heappush(pq, (heightMap[0][j], 0, j))
            heappush(pq, (heightMap[m-1][j], m-1, j))
            vis.add((0, j))
            vis.add((m-1, j))

        directions = [(1,0),(-1,0),(0,1),(0,-1)]
        ans = 0      #water_trapped
        max_height = 0
        while pq:
            h, i, j = heappop(pq)     # h - height
            for di, dj in directions:
                ni, nj = i + di, j + dj
                if 0 <=ni < m and 0 <=nj < n and (ni,nj) not in vis:
                    vis.add((ni, nj))
                    ans += max(0, h - heightMap[ni][nj])
                    max_height = max(h, heightMap[ni][nj])
                    heappush(pq, (max_height, ni, nj))
        return ans

equivalency

...
for i in range(m):
    heappush(pq, (heightMap[i][0], i, 0))
    heappush(pq, (heightMap[i][n-1], i, n-1))
    vis.add((i, 0))
    vis.add((i, n-1))

for j in range(n):
    heappush(pq, (heightMap[0][j], 0, j))
    heappush(pq, (heightMap[m-1][j], m-1, j))
    vis.add((0, j))
    vis.add((m-1, j))
...
            ||
            ||
            ||
...
for i in range(m):
    for j in [0, n-1]:
        heappush(pq, (heightMap[i][j], i, j))
        vis.add((i, j))

for j in range(n):
    for i in [0, m-1]:
        heappush(pq, (heightMap[i][j], i, j))
        vis.add((i, j))
...

There could be many other ways or writing styles, but I prefer mine